(April 1999)

von

Wer glaubt, gewisse Begriffe seien schlechtweg die richtigen, wer andere hätte, sähe eben etwas nicht ein, was wir einsehen, - der möge sich gewisse sehr allgemeine Naturtatsachen anders vorstellen, als wir sie gewohnt sind, und andere Begriffsbildungen als die gewohnten werden ihm verständlich werden (L. Wittgenstein. Philosophische Untersuchungen, 3. Aufl. Frankfurt a. M. 1982, S. 368)

Der Begriff der "Familienähnlichkeit" ist durch Wittgensteins Spätphilosophie in der Logik notorisch geworden. Wittgenstein demonstrierte, was er damit meinte, vor allem am Begriff der Sprache, dem des Spieles und am Sprachspiel. Er meinte, es ließen sich keine allgemeinen Merkmale für alle Sprachen, Spiele und Sprachspiele herausstellen. Einige Spiele hätten zwar mit gewissen anderen gemeinsame Merkmale, aber mit wiederum anderen überhaupt keine. Und das zeige, daß "familienähnliche" Begriffe keine "universalen", d. h. für alle Einzelbeispiele gemeinsam zutreffende Merkmale enthielten.¹ An die Stelle identischer Merkmale setzte Wittgenstein für die Begriffsbildung daher "ähnliche" Merkmale. Aber er hat nicht geklärt und offensichtlich nicht einmal als Problem empfunden, was hier "ähnlich" heißt. Wir können aber schon jetzt feststellen, daß er mit der Ähnlichkeit ein dialektisches Moment in seine Sprachlogik eingeführt hat, dessen Folgen weder von ihm noch von seinen Anhängern durchschaut worden sind. Warum Wittgenstein darin kein Problem sah, läßt sich vielleicht auf drei Motive zurückführen, nämlich sein vom "Tractatus" her eingeübtes mathematisches Denken, die Verbreitetheit des Analogiedenkens in der Methodologie, und schließlich seine Orientierung der Logik an grammatischen Strukturen in der Spätphilosophie. Betrachten wir zunächst, was er von daher in sein Logikkonzept übernahm.

1. Unter der unausgesprochenen Voraussetzung, die schon seine Logik des "Tractatus" geprägt hatte, daß nämlich mathematische Denkformen die eigentlichen logischen Denkformen seien, importierte er in die "Familienähnlichkeit" die Verschmelzung von Gleichung und Ungleichung in dem "mathematischen Junktor" der Form "...   ..." oder "...   ..." (gelesen: "... kleiner/gleich ..." bzw. "... größer/gleich ..."). Ersichtlich gibt es unter den logischen Junktoren bisher keinen, dessen Explikation diese mathematische Denkform (wir nennen sie einen mathematischen Junktor) sein könnte. Der vorsichtige Logiker würde vielleicht dazu neigen, diesen Junktor als "entweder kleiner oder gleich" bzw. "entweder größer oder gleich" zu lesen. Aber eine solche alternative Verknüpfung wird hier mathematisch nicht notiert und ist auch nicht gemeint. Vielmehr ist der Sinn die adjunktive Verknüpfung von "gleich und ungleich" als Wertebereich einer Variablen. Der (nicht immer notierte) Querstrich läßt diese Festlegung im Unklaren. Das deutet auf eine gewöhnlich von mathematischen Logikern übersehene "dialektische" Denkform für Widersprüchlichkeiten hin.²

Daß die "Familienähnlichkeit" auch bei vielen Geisteswissenschaftlern gut aufgenommen wurde, dürfte an der Verbreitung des Analogiedenkens liegen, das auch von Wittgenstein praktiziert wurde. Von Thomas von Aquin wurde die aristotelische These, daß der Seinsbegriff durch die Kategorien "pollachos legethai", d. h. "in vielfältiger Weise ausgesprochen" werde, so interpretiert, daß das Wesensmerkmal des Seinsbegriffs (als generisches Merkmal) nicht als identisches, sondern nur als "ähnliches" Merkmal in die Kategorien eingehe. Deshalb werde das "Sein" der Substanzen" zwar auch "Sein" genannt, es sei aber ein anderes Sein als in den Akzidentien, also den Qualitäten, Quantitäten, Relationen usw. Und diese Eigenschaft nannte Thomas "Analogie". Logisch gesehen handelt es sich hier um eine Fassung des Seinsbegriffs, die ihn zu einer contradictio in adiecto macht: Das Sein ist "Sein", aber zugleich auch "Nicht-Sein". Duns Scotus hat diese Analogielehre bekämpft und darauf bestanden, daß das generische Merkmal der Gattung Sein "univok" (d. h. in stabiler identischer Bedeutung) in alle Kategorien eingehe, wie es ja auch jede andere normale Begriffsbildung vom "genus proximum und differentia specifica" her zeige. Der "vielfältige Ausdruck" der Gattung in den Arten kann dann nur die Tatsache bezeichnen, daß das "univoke" (identische) generische Merkmal durch die spezifischen Differenzen ergänzt und weiter bestimmt wird. Thomas von Aquin hatte die Begriffsanalogie auf die höchsten metaphysischen Begriffe beschränkt, und dies vor allem in dem theologischen Interesse, die Transzendenz des Göttlichen und seiner "andersartigen" Seinsweise gegenüber der geschaffenen Welt und ihrem Sein zu wahren. Auch die Familienähnlichkeitsfreunde unter den Geisteswissenschaftlern neigen offensichtlich dazu, den neuen Begriff auf ausgezeichnete Probleme der Philosophie zu beschränken, bei denen man mit normalen Begriffen nicht recht weiterkommt.

Das dritte Motiv des Wittgensteinschen Familienähnlichkeitsbegriffs dürfte von seinem gemeinsprachentheoretischen Logikkonzept herrühren. Wenn nach diesem Konzept die Logik nur diejenigen Strukturen festhält, die sich in der Alltagssprache zeigen, so sollte auch die grammatische Homonymie eine logische Rolle spielen. Wittgenstein hat sie entgegen der Warnung schon des Aristoteles, daß sie die Quelle von Widersprüchen sei, als logische Normalform der Begriffsbildung in die Logik aufgenommen. Damit entstand ihm das Forschungsprogramm, das logische Verhältnis des sprachlich gleich Benannten und zugleich sachlich genau Unterschiedenen in einer logischen Form zu fixieren. Er formulierte es als "Familienähnlichkeit".

Aus dem Gesagten geht hervor, daß man bei einer logischen Analyse der "Familienähnlichkeit" von Begriffen auf widersprüchliche Elemente stoßen dürfte, die man umso genauer kennen muß, als man erst dadurch dasjenige, was nicht widersprüchlich an ihnen ist, abgrenzen und herausstellen kann.

2. Wie unterscheiden sich "familienähnliche" Begriffe von den normalen Allgemeinbegriffen? Schon auf den ersten Blick muß auffallen, daß familienähnliche Begriffe stets im Plural auftauchen, gewöhnlich aber als Paare. Es gibt nicht "den familienähnlichen Begriff", sondern nur mehrere oder mindestens zwei, die eine "Familienähnlichkeit" aufweisen. Wittgenstein gewinnt sie ja aus der Vergleichung von solchen Sprachspielen, in denen sie unter demselben Terminus, aber mit verschiedener Bedeutung, vorkommen. Normale logische Begriffe aber können wesentlich in der Einzahl vorkommen.

Normale logische Begriffe fixieren als ihre Bedeutung (Intension) ausschließlich die gemeinsamen Merkmale der in ihrer Extension liegenden Gegenstände. Diese Merkmale bezeichnen daher ein im Allgemeinbegriff und in allen seinen Art- und Unterbegriffen bzw. individuellen Instanzen Identisches. Bei der Bildung solcher normalen Begriffe geht man offensichtlich auch von Ähnlichkeiten aus, die sich im Instanzenmaterial finden. Die Ähnlichkeiten zwischen denselben bilden gewissermaßen einen heuristischen Leitfaden für die Zusammenstellung und Gruppierung der Instanzen hinsichtlich ihrer begrifflichen Ordnung. Aber die Begriffsbildung selbst beruht eben darauf, in den angetroffenen Ähnlichkeiten exakt und streng zwischen zwei Komponenten der Ähnlichkeit zu unterscheiden und diese "auf den Begriff zu bringen". Die eine Komponente ist nichts anderes als "dasselbe", d. h. die Identität am Ähnlichen; die andere Komponente ist die Verschiedenheit bzw. Unterschiedlichkeit am Ähnlichen. Das Identische wird als Gemeinsames im Ähnlichen herausgehoben und als "Allgemeines" in der Gattung fixiert. Das Unterschiedliche wird in den sog. spezifischen Differenzen festgehalten und in den Art- und Unterartbegriffen, die zu einem Allgemeinbegriff (Gattung) gehören, fixiert.

Im Gegensatz dazu sollen die familienähnlichen Begriffe im wesentlichen Fall gerade keine identischen Merkmale, sondern nur "ähnliche" Merkmale fixieren, die sich an den Gegenständen in ihrer Extension finden. Ähnliche oder, wie man mit den Analogiedenkern sagen kann, analoge Merkmale hat es bisher in der logischen Begriffslehre aber nicht gegeben. Und so hat man in der Behauptung Wittgensteins, daß es sie gebe, die wesentliche logische Neuerung zu sehen.

Die logische Frage ist hier, ob solche behaupteten "ähnlichen" Merkmale tatsächlich existieren. Ähnlichkeiten pflegen bei der Betrachtung von Instanzen gleichsam in die Augen zu springen, aber wer die Ähnlichkeiten beobachtet, weiß gewöhnlich auch, daß sie, wie man üblicherweeise sagt, auf etwas "Gleiches" und zugleich auf etwas "Ungleiches" an den ähnlichen Dingen hinweisen. Was man sprachlich das "Gleiche" nennt, ist aber eine logische Identität, und das sprachlich "Ungleiche" eine logische Verschiedenheit. Hat man sich das klargemacht, so hat man die Ähnlichkeit schon analysiert und ist gleichsam unter sie hinabgestiegen. Wo es um normale Begriffsbildung geht, ist dies immer der Fall. Die Frage kann dann nur sein, ob man mit den Ähnlichkeiten im Instanzenmaterial bei der Begriffsbildung noch auf andere Weise umgehen kann, als wie für die normale Begriffsbildung beschrieben wurde. Dies scheint der Fall zu sein und verdient daher, noch genauer herausgestellt zu werden.

3. Das logisch Neuartige und Bemerkenswerte bei der Bildung familienähnlicher Begriffe liegt darin, daß dadurch eigentlich zwei normale Begriffe, die in einem privilegierten Bezug zueinander stehen, in einem speziellen Induktionsverfahren zugleich gewonnen, definiert und in ihrem Verhältnis zueinander festgehalten werden. Ersichtlich sind deshalb die Induktionsverfahren der normalen und der Familienähnlichkeitsbegriffe verschieden. Diesen Unterschied wollen wir zunächst herausstellen.

Die normale Induktion³, gewöhnlich auch Abstraktionsverfahren genannt, gewinnt erst einmal einen "Induktionsrahmen" durch die Feststellung eines in beliebigen Instanzen identischen Merkmals und hält ihn in einem Gattungsbegriff als dessen Merkmal fest. Der Gattungsbegriff des Induktionsrahmens fixiert damit ein "generisches Merkmal", von dem - dann gewissermaßen apriori - feststeht, ob es gewissen Instanzen zukommt oder nicht zukommt. Dadurch wird auch die Extension dieses Gattungsbegriffes festgelegt. Die berühmten "möglichen Fälle" bzw. Instanzen enthalten sämtlich dieses generische Merkmal. Diejenigen Instanzen, die das Merkmal nicht enthalten, sind daher auch nicht als "mögliche" Fälle, sondern als "nichtmögliche" Fälle zu bezeichnen. Erst innerhalb dieses Induktionsrahmens unterscheiden sich die möglichen Fälle nach spezifischen Merkmalen und lassen sich so in Arten und Unterarten der Gattung einteilen.

Es sei bei dieser Gelegenheit daran erinnert, daß das seit Aristoteles übliche Definitionsverfahren regulärer Begriffe darin besteht, das "Genus proximum und die differentia specifica" des zu definierenden Begriffs anzugeben. Die Epagogé (lat. inductio) ist also darauf gerichtet, im Merkmalsbestand des zu definierenden Begriffs die "generischen" Merkmalsbestände, die von der übergeordneten Gattung herstammen und mit dem gesamten Merkmalsbestand dieser Gattung identisch sind, sowie die spezifischen (zusätzlichen) Merkmale, die den zu definierenden Begriff von der Gattung als auch von den anderen, unter dieselbe Gattung fallenden Begriffen unterscheiden, deutlich herauszustellen. Die "nächsthöhere Gattung" (und genau genommen: alle höheren Gattungen), in deren Umfang der zu definierende Begriff stehen muß, liefert also das gemeinsame Merkmal (oder die gemeinsamen Merkmale) aller in seinen Umfang fallenden Instanzen und ist durch seine Extension zugleich das, was wir hier "Induktionsrahmen" nennen. Daß die Definition eines Begriffes als spezifischer Artbegriff immer schon die Festsetzung seiner zugehörigen Gattung (d. h. natürlich ihrer Merkmale und ihres Umfangs) voraussetzt, ist jedem Logiker bekannt, aber in den üblichen Induktionstheorien nicht genügend beachtet worden.

Das reguläre Induktionsverfahren läßt sich folgendermaßen darstellen, wenn wir bei den Instanzen jeweils drei Merkmalen von fünf insgesamt konstatierbaren Merkmalen ins Auge fassen:

Merkmale Beispiele

A = Schwanengestalt

B = männlich

C = weiblich

D = weiß

E = schwarz

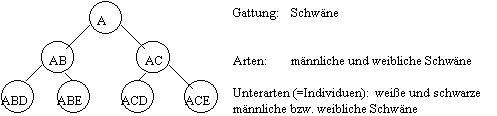
Individuen: ABD ABE ACD ACE (Individuen sind "Träger" von Merkmalskomplexen. Über die Anzahl der Individuen wird nichts festgestellt).

Induktionsrahmen (angezielter Gattungsbegriff) hat das in jedem Individuum vorkommende Merkmal: A = "Schwanengestalt".

Artbildende spezifische Differenz kann jedes Merkmal sein, das sich nur bei einigen, d. h. also nicht allen Individuen findet.

Induzierte Begriffsstruktur bei Wahl des Geschlechtscharakters als artbildene Differenz:

Figur 1

4. Die Induktion der familienähnlichen Begriffe verschmäht nun einen solchen Induktionsrahmen mit der Ausgangsthese, es gäbe in den wesentlichen Fällen überhaupt kein gemeinsames (Gattungs-)Merkmal, und mit der zusätzlichen (davon abhängigen) These, es stünde ja nicht fest, was alles zur Familie gehöre. Hierin liegt aber selbst schon eine Unklarheit: Wenn man von Familie redet, steht natürlich fest, wer dazu gehört, und "Familie" ist schon ein Induktionsrahmen, wie weit man ihn auch ziehen mag. Legt man bei einer tatsächlichen Familie Wert darauf, auch adoptierte und uneheliche Kinder und evtl. sogar den Hausfreund zur Familie zu zählen, so ist auch dadurch die Familienzugehörigkeit als Induktionsrahmen schon etabliert und alle "möglichen" Mitglieder lassen sich nach spezifischen Differenzen in Arten - evtl. nach den "echten" und den "unechten" Mitgliedern - einteilen. Die Ausgangsthese Wittgensteins und der Analytiker, die ja den Familienbegriff selbst nur in analoger bzw. metaphorischer (d. h. familienähnlicher) Weise verwenden, ist dagegen, der Mitgliederbereich bliebe gleichwohl unbestimmt. Sie können sich für diese (falsche) Meinung auf die üblichen Induktionstheorien Humescher Art berufen, nach welchen ja niemals empirisch "alle Fälle" abschließend darauf hin geprüft werden können, ob sie das generische Merkmal besitzen und ob sie damit in den Induktionsrahmen passen oder nicht. Demgegenüber ist aber mit Francis Bacon daran zu erinnern, daß in der Logik nicht gezählt wird, so daß eine zahlenmäßige Bestandsaufnahme von Individuen, die Träger gewisser Merkmale sind, kein logisches Argument für die Begriffsbildung darstellen können. Im Zweifelsfall genügt dafür, wie schon Wilhelm von Ockham betont, ein einziger Beispielsfall als Induktionsbasis. Die angebliche Unbestimmtheit des Induktionsrahmens in der Familienähnlichkeitstheorie kann aber nur bedeuten: "Familie" ist bei der Induktion familienähnlicher Begriffe zugleich die Gattung und auch nicht die Gattung. Und dies verweist wiederum auf einen Widerspruch in den Grundlagen dieser Theorie.

Nota bene: wir meinen, daß bei "Familie" die "Familienzugehörigkeit" immer schon das allgemeine Gattungsmerkmal ist, und daß dadurch genau festgelegt wird, wer zur Familie gehört und wer nicht. Das gilt ebenso im empirischen Bereich der menschlichen Familien, wie im Bereich logischer "Familien", wo "Familie" nur ein anderer Terminus für eine bestimmte Menge oder Klasse ist. Und deshalb halten wir die Wittgensteinsche und analytische Voraussetzung, familienähnliche Begriffe hätten (in den wesentlichen Fällen) kein gemeinsames Merkmal, für falsch. Es ist derselbe Fehler, den schon J. St. Mill begangen hat, als er übersah, daß der Gattungsbegriff "Schwan" schon als Induktionsrahmen induziert sein mußte, ehe man die dann sekundäre Frage behandelte (die Mill für die eigentliche Induktionsfrage hielt!), ob alle Schwäne weiß seien, oder ob es noch andersfarbige gäbe.⁴ Nur weil man die Gattung "Schwan" schon induziert hatte, konnte überhaupt die Frage ins Auge gefaßt werden, ob auch schwarze Schwäne Schwäne seien oder ob sie nicht zu einer anderen Gattung von Tieren gehören.

In gleicher Weise setzt auch die Induktion familienähnlicher Begriffe schon einen Induktionsrahmen voraus, der durch "Familie" bei Wittgenstein freilich nur undeutlich bezeichnet wird. Er wird von Wittgenstein nur nicht beachtet, und zwar wie beim Schwanbegriff Mills aus dem schlichten Grunde, weil er den Wald der Instanzen vor lauter Bäumen der familienähnlichen Merkmale nicht sieht.⁵ Innerhalb dieses Induktionsrahmens wird nun bei der Familienähnlichkeit eine doppelte Induktion auf zwei allgemeine Begriffe von der gemeinsamen Induktionsbasis der Instanzen aus vorgenommen. Diese beiden Begriffe können logisch nichts anderes sein als zwei Artbegriffe unter der Gattung der Familienzugehörigkeit.

Diese doppelte Induktion ist nun das neue und verblüffende Element der Wittgensteinschen Begriffslehre, das noch nicht genügend durchschaut ist. Und es ist kein Zufall, daß dafür die "Familie" das Denkmuster geliefert hat. Von ihr weiß man und setzt man voraus, daß eine Merkmalsmenge von der mütterlichen, eine andere von der väterlichen Seite herstammen muß, und die müssen sich genau unterscheiden lassen. Das auffälligste Merkmal der mütterlichen Seite ist nun in der "Familie" zweifellos das weibliche Geschlecht, und von der Vaterseite her das männliche. Daneben mag es beliebig viele andere Merkmale von der mütterlichen oder väterlichen Seite her geben. Auf jeden Fall liefert der Geschlechtsunterschied in der wirklichen Familie die immer vorhandenen gegensätzlichen Merkmale. Das macht suggestiv darauf aufmerksam, daß es bei der "Familienähnlichkeit" zumindest ein Merkmal gibt, das nicht alle Familienmitglieder zugleich besitzen können.

Die doppelte Induktion von derselben Induktionsbasis ("Familie") aus richtet sich nun auf die Gewinnung der beiden (am ehesten "typologisch" zu nennenden) Art-begriffe. Wir können als das dominierende Muttertypische das Merkmal "Weiblichkeit" nehmen, als das dominant Vatertypische "Männlichkeit". Wir bemerken ausdrücklich, daß man an Stelle des Geschlechts auch jedes andere für die eine oder die andere Seite typische Merkmal nehmen könnte, so daß dann das Geschlecht nur als nachgeordnetes Merkmal oder überhaupt nicht berücksichtigt würde.

Welche Merkmale dienen nunmehr als spezifische Merkmale und somit zur weiteren Einteilung von Unterarten und gegebenfalls Unter-Unterarten der Eigenschaftskombinationen der Familienmitglieder? Logischerweiser nur solche, die man überhaupt an den Instanzen ablesen kann. Bei der Familienähnlichkeit interessieren aber nur solche, die überhaupt im Bereich der Familientypik liegen, also speziellere Merkmale des Vaters oder der Mutter. Das führt dazu, daß bei dieser Doppelinduktion bei den muttertypischen Arten väterliche Merkmale und umgekehrt bei den vatertypischen Arten mütterliche Merkmale als spezifische Merkmale ausgezeichnet werden. Diese wechselseitige spezifische Determination des einen Induktionsbegriffs durch die Merkmale des anderen Induktionsbegriffs ist nun dasjenige, was die Familienähnlichkeit in der Tat von den normal induzierten Begriffen unterscheidet, bei denen man - wie oben und in meiner "Logik" ausführlicher gezeigt - beliebige Merkmale aus den gemeinsamen Merkmalen der Fälle als einzigen Induktionsrahmen vorgeben kann.

Die Doppelinduktion der "Familienähnlichkeit" erklärt nun erst einmal zwanglos, warum nach Ansicht Wittgensteins die Familienmitglieder in Hinsicht auf die "Familienähnlichkeit" nicht wenigstens ein Merkmal gemeinsam haben müssen (obwohl wir immer noch behaupten, die "Familienzugehörigkeit" sei eben schon dies gemeinsame Merkmal). Die normale Familie ist immer schon durch den Geschlechtsunterschied von Mutter und Vater und der Kinder als auffälligem Merkmal bestimmt, und alle Familienmitglieder sind jeweils entweder weiblich oder männlich, aber nicht beides zugleich. Der empirische Geschlechtsunterschied in der Familie wird offenbar zum logischen Modell für die Forderung der nichtgemeinsamen Merkmale in der logischen "Familie". Man hat sich aber sehr davor zu hüten, "Mutter", "Vater", "Mädchen" und "Jungen" für logische Individuen und "weiblich" und "männlich" für ebenso logische nichtgemeinsame wesentliche Merkmale auch in der logischen "Familie" und überhaupt bei der Begriffsbildung zu halten. In der Logik sind Individuen nichts anderes als "unterste Merkmalskomplexe" in porphyrianischen Begriffstrukturen, und was wesentliche Merkmale sein sollen, ist durchaus eine Sache dessen, was man für wichtig hält und besonders beachten will.

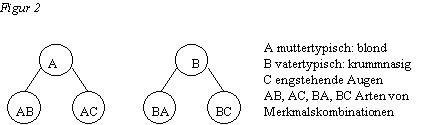
Machen wir uns das bisher Gesagte an einem Beispiel deutlich, das durch R. Bambrough⁶ berühmt geworden ist, und das wir noch etwas vereinfachen. Beachten wir bei den Familienmitgliedern einer Familie nur drei Merkmale: A, B und C. A bezeichne etwas zufällig "Muttertypisches", z. B. "blond". B bezeichne etwas zufällig "Vatertypisches", z. B. "krummnasig". C bezeichne ein beliebiges weiteres Merkmal, z. B. die enge zusammenstehenden Augen, die sich wiederum zufällig bei der Mutter finden mögen. Die Reihe der Merkmalskombinationen, die einzelne Familienmitglieder aufweisen können, sieht also folgendermaßen aus:

AB AC BA BC

Man sieht, daß sich die Merkmale überlappen, und daß kein Merkmal in allen Kombinationen gemeinsam vorkommt. Außerdem zeigt sich, daß sich A und B als getrennte, d. h. doppelte Induktionsrahmen anbieten, innerhalb derer jeweils zwei Kombinationen als Arten spezifiziert werden können. Die doppelte Induktion führt also zu zwei Begriffen, deren sog. generisches Merkmal beim entgegengesetzten Begriff als spezifische Differenz zur Artunterscheidung dient. Wir stellen diese Familienähnlichkeits-induktion in pyramidaler Notation folgendermaßen dar:

Es dürfte logisch klar sein, daß diese logische Betrachtung nichts über die Zahl der Familienmitglieder beeinhaltet. Überhaupt bezieht sich diese Induktion ja nicht auf Personen und Personenbegriffe, sondern auf den Begriff der Familienähnlichkeit, der als solcher nichts über Menschen, Personen, Dinge als Individuen besagt, sondern über gewisse Eigenschaften und ihre Kombinationen an solchen.

Wir haben diese Doppelinduktion nach allen Regeln der klassischen einfachen Induktion durchgeführt, und darin liegt zunächst das leicht Verständliche und Übliche, was die Analytiker und wohl auch Wittgenstein selbst veranlaßte zu meinen, es handele sich dabei um übliche Begriffsbildung bzw. logische Begriffe seien überhaupt "Familienähnlichkeiten". Bei dieser Doppelinduktion treten nun die beiden induzierten Allgemeinbegriffe in ein besonderers Verhältnis zueinander, das man polar nennen könnte. Wie wir voraussetzten, müssen die beiden Induktionsbegriffe reguläre Artbegriffe unter einem gemeinsamen Oberbegriff - nämlich der "Familienzugehörigkeit" - sein. Ebenso ersichtlich handelt es sich aber nicht um dihäretische Nebenarten - obwohl man bei Begriffen wie "Familie", "Vatertypisches" und "Muttertypisches" an die dihäretische Geschlechtsunterscheidung denkt. Diese spielt aber, wie schon betont, bei der logischen Familienähnlichkeit keine Rolle. Das sieht man daran, daß sich leicht auch "Ähnlichkeiten" in dreifacher und mehrfacher Induktion auf Begriffe bringen lassen, was die logische Lage allenfalls kompliziert, aber nicht grundsätzlich ändert. Stehen die beiden induzierten Artbegriffe vom Muttertypischen und Vatertypischen aber nicht im dihäretischen Verhältnis zueinander (d. h. sie bilden keine vollständige Disjunktion), so kann die eine Art nicht das "kontradiktorische" Gegenteil der anderen bilden, d. h. sie stehen nicht in bestimmter, sondern in unbestimmter Negation zueinander.⁷ Dies ist wiederum die logische Bedingung dafür, daß die Merkmalsgruppe AB keine contradictio in terminis bildet, sondern eine schlichte Spezifikation (hier A = generisches Merkmal, B = spezifische Differenz) bezeichnet.

5. Handelt es sich aber bei der doppelten Induktion um zwei (von beliebig vielen multiplen) Artbegriffen, auf die hin induziert werden kann, so muß es, wie schon mehrfach betont, aus logischen Gründen einen gemeinsamen Oberbegriff über diesen Artbegriffen, also ihre Gattung geben. Er ist auch durch die Bezeichnung "Familie" im Familienähnlichkeitsbegriff vorbezeichnet. Aber man läßt sich zu leicht verleiten, diesen als eine reine Extensionsangabe für die Individuen, die zu einer Familie gehören, anzusehen anstatt als intensionales Merkmal, welches zugleich auch die Extension des Induktionsrahmens festlegt. Genauer haben wir ihn schon als "Familienzugehörigkeit" bezeichnet. Und hält man sich logisch daran, so ist damit auch ein Merkmal festgestellt, das alle zugehörigen Fälle eindeutig bestimmt und schließlich das gemeinsame Merkmal aller Fälle ausmacht. In diesem Punkte schließt auch die Doppelinduktion wieder an die einfache und normale Induktion an und macht sie dadurch zu einem Spezialfall der normalen Induktion. Notieren wir ein solches Merkmal X (z. B. für den Familiennamen der Familie "Xaver" stehend) zu allen Merkmalskombinationen hinzu, so sieht unsere pyramidale Notation der Doppelinduktion der Familienähnlichkeit - wie es nicht anders sein kann in einer effektiven Logik - folgendermaßen aus:

Es dürfte auf der Hand liegen, daß die wesentliche logische Neuerung und Fruchtbarkeit der Wittgensteinschen "Familienähnlichkeit" bei Begriffen in der Entdeckung der logischen Definitionsweise von polar einander zugeordneten Begriffen durch die Merkmale des jeweils gegenpoligen Begriffes liegt. Die Ausarbeitung dieser Methode der "Doppelinduktion" oder gar einer mehrpoligen "Tupelinduktion" dürfte die begriffslogische Methodologie mancher Wissenschaftsbereiche wesentlich bereichern können. Aber um dies zu klären und dazu beizutragen, bedarf es, wie aus dem Vorangehenden deutlich geworden sein dürfte, logischer Notationsinstrumente, die bisher nicht zur Verfügung standen. Erst diese erlauben es aber auch erst, in Wittgensteins Konzept der Familienähnlichkeit von Begriffen den logischen Weizen von der Spreu zu trennen. Letztere aber scheint zu einer Verbreitung und Verstärkung von dialektischem Denken zu führen nicht nur bei denjenigen Wittgensteinverehrern, die ohnehin nicht viel mit Logik anfangen können, sondern auch bei gestandenen Analytikern. Diesen Aspekt der Wittgensteinschen Lehre wollen wir im folgenden noch etwas beleuchten.

6. Der Einschuß von Widersprüchlichkeit und damit das Paradoxale an der Familienähnlichkeitstheorie beruht, wie oben schon öfter berührt, darauf, daß es nach Meinung Wittgensteins und der Analytiker ein gemeinsames Merkmal aller Instanzen und damit auch einen allgemeinen Induktionsrahmen für das Doppelinduktionsverfahren nicht geben soll, obwohl sie entsprechendes immer schon vorausgesetzt haben.⁸ Dementsprechend sollte sich auch an keinem (empirischen) Fall das Merkmal "Familienzugehörigkeit" zeigen, obwohl doch offensichtlich die Familienzugehörigkeit das Auswahlkriterium für die relevanten Fälle von familienähnlichen Merkmalskombinationen darstellt.⁹ "Familienzugehörigkeit" wird dadurch zugleich als Merkmal und nicht als Merkmal behandelt, und das erweist die Dialektik der Wittgensteinschen Familienähnlichkeitslogik.

Es ist aus logischen Gründen klar, daß die Vertreter dieser Art von Begriffen ohne klare Intensionen und Extensionen überhaupt das logische und induktive Prozedere verschmähen und daher nach Belieben alles und jedes oder auch gar nichts als "zur Familie gehörig" erklären können. Das sieht man in der analytischen Literatur und in Wittgensteins Schriften. Aber sie widersprechen sich und ihrer eigenen Meinung schon dadurch, daß sie an die Stelle der "Familienzugehörigkeit" in allen Beispielen einen sehr präzisen Begriff setzen, der eben das die Familienzugehörigkeit ausmachende Merkmal angibt: nämlich die "Benennung" dessen, was im Sprachspiel familienähnliche Merkmale aufweisen soll, selbst. Das Vorhandensein eines Wortes, einer Benennung in einer Sprache dient ihnen bei ihrem gemeinsprachentheoretischen Ansatz schon als oberster Induktionsrahmen für die beiden gedoppelten Teilinduktionen. Das schließt natürlich alle Homonyme ein und verstößt, wie oben schon gesagt, gegen eine Warnung, die schon Aristoteles in seinem Organon für alle logische Begriffsbildung ausgesprochen hat: Hinter sprachlichen Homonymien verbergen sich begriffliche Unterscheidungen, die zu beachten sind. Genau dagegen verstoßen nun die Familienähnlichkeitsfreunde. Sie wollen auch noch die entlegensten Sachverhalte unter einen "Familienähnlichkeitsbegriff" bringen, wenn sie nur eine gemeinsame Bezeichnung haben.

So mag die Familie von Herrn Müller und die Familie eines anderen Herrn Müller, der mit ersterem verwandt sein mag oder nicht, gewiß eine Menge gemeinsamer Merkmale und auch unterschiedlicher Merkmale aufweisen. Und dasselbe gilt von allen Familien, seien es nun "Familien" von Menschen, Pflanzen, Tieren oder Mineralien. Die "Familienähnlichkeit" erlaubt in der Tat, in allen diesen wohlbestimmten Umkreisen Gemeinsamkeiten und Unterschiede herauszustellen. Das heißt aber nichts anderes, als den Gattungsbegriff "Familie" unter der Hand durch einen allgemeineren Begriff zu ersetzen. Und in der Tat wird er letztlich der Begriff der "Ähnlichkeit" selber sein. Das aber führt uns auf die Ausgangsfrage zurück nach dem logischen Charakter der "Ähnlichkeit" selber.

7. "Ähnlichkeit" als logischer Begriff betrachtet, bedeutet eine kontradiktorische Verschmelzung von Selbigkeit und Verschiedenheit, oder präziser ausgedrückt: von Identität und Nichtidentität. Wenn etwas einem anderen ähnlich sein soll, so muß es sich von diesem anderen unterscheiden lassen und zugleich mit ihm in (mindestens einem) Merkmal übereinstimmen. Identität wird logisch durch gemeinsame Merkmale im Verschiedenen erfaßt, Nichtidentität durch verschiedene Merkmale im Verschiedenen. Traditionellerweise drückt man die Identität durch den aus unterschiedenen Arten oder Unterarten abstrahierten Gattungsbegriff aus, die Nichtidentität aber durch die unterschiedenen Arten und Unterarten dieser Gattung. "Ähnlichkeit" muß als daraus Verschmolzendes zugleich Gattungs- und Artbegriff sein und sich zugleich von den regulären Gattungs- und Artbegriffen unterscheiden.

Ein solcher Begriff ist nichts anderes als eine Contradictio in terminis. Die Logiker tun sich damit bisher noch schwer. Man unterstellt, kontradiktorische Begriffe hätten keine Bedeutung, seien "sinnlos", Ausdruck des "Absurden", aber auch des "Falschen", zugleich spricht man davon, daß ihre Extension "Nichts" sei. Das paßt sicherlich nicht zusammen und klingt seinerseits recht widerspruchsvoll. Gleichwohl haben auch diese widersprüchlichen Begriffe eine logische Form. Als Begriffe können sie schon deswegen nicht "falsch" sein, weil sich Falschheit in der Logik nur in Urteilen kundgeben kann. "Absurdes" können sie schon deswegen nicht ausdrücken, weil damit auf etwas Unverständliches abgestellt würde, was keineswegs noch zur Logik gehören könnte. Und in der Tat ist ja der Widerspruch und alles Widersprüchliche sehr wohl ein logisches Element und als solches verständlich.

Setzt man "Nichts" als Extension widersprüchlicher Begriffe, so hat man dadurch schon aus logischen Gründen das Nichts zu einem wohlbekannten Gegenstand erklärt, der nur durch widerspruchsvolle Begriffe erfaßt werden soll. Die Mathematiker gehen mit diesem "Nichts" seit langem um: Es ist die Extension des Zahlbegriffs "Null" bzw. die Extension der "leeren Menge". Daß diese mathematischen Denkformen etwas Widersprüchliches an sich haben, ist lange empfunden, aber ebenso beharrlich geleugnet worden. Die Null kann man logisch eine Zahl und zugleich eine Nicht-Zahl nennen, und die leere Menge sowohl eine Menge wie auch eine Nicht-Menge. Daß sich aus solchen "Begriffen" arithmetische und mengentheoretische Paradoxien ergeben müssen, müßte für jeden Logiker auf der Hand liegen. In der "mathematischen Logik" werden diese Paradoxien aber gewöhnlich als durch weitere Forschung zu eliminierende Probleme gehandelt. In der Tat ist ein kontradiktorischer Begriff eine Verschmelzung aus zwei dihäretischen Artbegriffen unter einer gemeinsamen Gattung derart, daß die im gegenseitigen Negationsverhältnis zueinander stehenden spezifischen Differenzen der verschmolzenen Artbegriffe zusammen mit den generischen Merkmalen der gemeinsamen Gattung in den Merkmalsbestand der Contradictio eingehen. Die Extension eines widerspruchsvollen Begriffes besteht dann in den gemeinsamen Extensionen der Ausgangsbegriffe, was so viel bedeutet, wie daß er keine eigene bzw. selbständige Extension besitzt. In pyramidaler Notation hat der widerspruchsvolle Begriff folgende Gestalt:

Hält man sich an Wittgensteins These, daß alle Begriffe familienähnlich seien, so kann das nur bedeuten, daß er alle Begriffe für dialektisch, d. h. für kontradiktorisch gehalten hat. Seine grammatologisch begründete Logik kann daher nichts anderes sein als eine dialektische Logik. Verwendet man seine familienähnlichen Begriffe als Prädikate in Urteilen, so müssen diese widersprüchlich werden. Wir können es so ausdrücken: Der Spielraum seiner Sprachspiele ist so groß und zugleich so klein, daß alles und Nichts hineinpaßt. Ist die Logik seines "Tractatus" noch geprägt von der Meinung, die mathematische Gleichung sei die exakte Gestalt des logischen Urteils¹⁰, in welchem (nach G. Frege) Subjekt und Prädikat als verschiedene Termini einen identischen Wert als Bedeutung des "Satzes" repräsentieren, so kehrt sich in der Familienähnlichkeitslogik das Verhältnis von Zeichen und Bedeutung geradezu um: gleiche Zeichen bedeuten Verschiedenes. Und das läßt sich nur als Ungleichung formalisieren: "X   X".¹¹ Das gilt dann explizit in der grammatologischen Logik seiner Spätphilosophie auch für das Verhältnis von Urteilskopula und mathematischem Gleichheitszeichen (Äquivalenzjunktor), denn beide werden als "ist" gelesen.¹² Beides zusammen aber etabliert in der neuen Sprachlogik die Denkform des "zugleich gleich und ungleich".

Wer also mit Wittgenstein Spiele spielt, der spielt zugleich nicht, denn es handelt sich ja angeblich um eine ernste Angelegenheit. Und wer sich auf Sprachspiele einläßt, der tut es in einer Sprache, die zugleich viele Sprachen sein soll - und die zuweilen keine Sprache ist, denn: "Wenn ein Löwe sprechen könnte, wir könnten ihn nicht verstehen." ¹³ In der Tat, Wittgensteins Logik der Sprachspiele redet in keinem anderen Sinn von Begriffen und Sätzen, als wir es im gewöhnlichen Leben tun, wenn wir etwa sagen "hier steht ein deutscher Satz aufgeschrieben" oder "nein, das sieht nur aus wie Schriftsprache, ist aber ein metasprachliches Zitat."¹⁴

War es bisher den Dichtern und ihrer kreativen Phantasie vorbehalten, die Familienähnlichkeiten (sprich: Analogien und Metaphoriken) zwischen dem Tau der Morgenfrühe und den Tauen der Schiffer (und evtl. dem chinesischen "Tau" der Taoisten) zu verworten, so wird das durch Wittgensteins Sprachlogik zum Geschäft der avancierten Wissenschaft. Und das zeigt, was es mit dieser Logik wirklich auf sich hat. Sie liefert eine willkommene Unterlage zur Methodologie des "anything goes", welche die moderne Wissenschaft dort, wo sie angewendet wird, zunächst der Lächerlichkeit preisgibt und sie schließlich zerstört.

====================================